The reason for comparing LPS against Space Domain is that Space Domain is the traditional textbook approach to pattern searching. It was hypothesized that, because LPS jumped around, it could find a pattern faster than Space Domain. It would take about the same amount of time for both algorithms to cover every pixel in an image, however with LPS, the pattern's neighborhood could be found before each pixel location was searched. Even if LPS doesn't find the exact center of the pattern before Space Domain, LPS would give a faster indication of where the pattern could be found within the image.
It's well known that Frequency Domain can be much faster than Space Domain; the speed up factor depends upon the ratio between image and subpattern size. For large ratios, i.e. a 3x3 correlation for a 500x500 image, it is faster to work in the space domain. In case the subpattern size is a large fraction of the whole image size, it is faster to work in the frequency domain). This increase in speed is based upon the number of operations (adding, multiplying, etc.) that need to be done. In this experiment, the Frequency Domain algorithm was used to compare against LPS for cases where the Frequency Domain was faster than Space Domain.
Random Ordering has a large chance of being faster than Space Domain or Frequency Domain. The ordering of pixels is guaranteed that every pixel location will be investigated.
Experiment 1 had five cases. The pattern sizes were: 3x3, 5x5, 11x11, 41x41, and 81x81 (all values are in pixel width and height). The image size was 500x500 pixels and consisted of a black rectangle (the pattern) on a white background. This first experiment was to see if LPS had any potential at all.
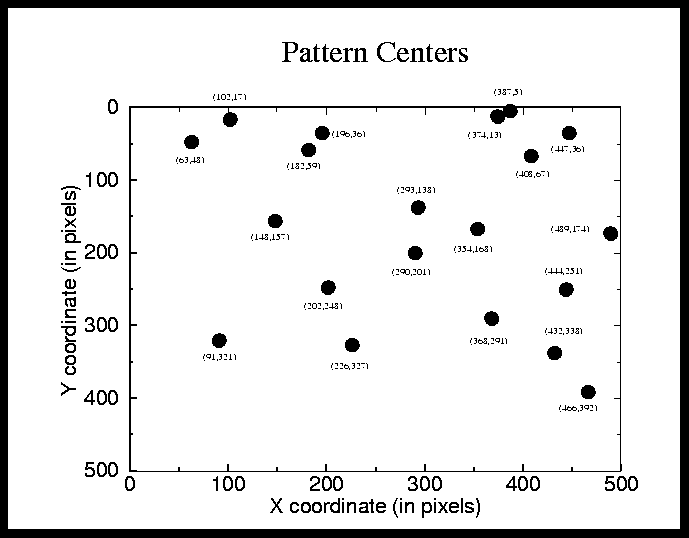
FIGURE 1. center positions for test cases in experiment 2
Experiment 2 had 20 cases. The pattern was chosen to be an 11x11 pixel square. The pattern size was chosen to be this large to give Random Ordering a chance. The center positions of the pattern can be seen in Figure 1 on page 4. The image size was 500x500 pixels and consisted of a black rectangle on a white background. This is to see if LPS is shift invariant or just lucky in Experiment 1 by jumping to the position in the image where the pattern was early in the execution.
Experiment 3 had one case (see Figure 2 on page 5). Unlike the first two experiments (in which the input data was computer generated with no noise), this experiment features a scanned page of text. The pattern to find is a circle on the text document. The circle was created by a rubber stamp. The image size was 612x792 pixels.
FIGURE 2. image for Experiment 3
For each experiment, each case ran using all four algorithms (Space Domain, Frequency Domain, LPS, and Random Ordering). The results were then plotted to compare distances (the Euclidean distance between where the object really was and where the procedure thought it was) and correlation values.
The distance values were plotted to see which algorithm found the pattern (or at least the area where the pattern was) the fastest.
Correlation values were plotted to see the semi-random progression of LPS compared to the other algorithms. In this type of graph, Space Domain and Frequency Domain would plot delta functions.
Sherlock was written in C using the XView toolkit on a Sun SPARCStation 4/40. Within Sherlock, two external routines were imported: a Fast Fourier Transform routine originally written in Fortran by Norman Brenner in 1968, which was translated to C by Keith Knox of Xerox Webster Research Center in September 1990; and timing macros by George V. Neville-Neil, Universiteit Twente (gnn@cs.utwent.nl). The software can run either in GUI mode or in batch mode. Batch mode can process commands from a file or interactively from the keyboard. Two result files are created for each algorithm run, the correlation results, and the distance results. An example plot of correlation values for LPS can be seen in Figure 3 on page 7. An example distance plot for all four algorithms can be seen in Figure 4 on page 8.
The correlation values are the amount of correlation between image and pattern at each pixel location within the image. These are not true correlation values in the sense of the Space Domain equation. In order to speed up processing, it was faster to find the difference (rather than the correlation) between image and pattern and then invert so that the maximum value showed the smallest difference. So, in effect, these values are really differences rather than correlations. The search index is the pixel ordering. A search index of 100 is the 100th pixel coordinate correlated. For Space Domain, this graph would show a delta function.
FIGURE 3. sample correlation output
The other results file is comprised of the Euclidean distance between where Sherlock thinks the pattern is and where it really is. Distance is mathematically defined as the distance between 2 points given by:
(EQ 1)
where (x0,y0) are the true coordinates of the pattern and (x1,y1) are the estimated coordinates.
FIGURE 4. sample distance output
When an algorithm starts, the estimated position of the pattern is set to (0,0). This means that if the pattern is near location (0,0), the distance will start off small as opposed to a pattern that is further away.
The results files are formatted to be read in with ACE/gr, a free 2D graphing program for exploratory data analysis (xvgr - Open Look\xaa or xmgr - Motif version) written by Paul Turner (of the Oregon Graduate Institute, email pturner@ese.ogi.edu). This enables the results to be graphed quickly.
After an algorithm has run, information about it is presented. In batch mode, it is written to the screen. In UI mode, a window pops up with the information (see Figure 5 on page 9). The information given is the same in either case. This includes:
In the case of LPS, the parameters (Parms) and the increments (Kn) used are given. In the case of Random Ordering, the seed (Seed) for the random number generator is given.
FIGURE 6. main Sherlock window
The button menus on the command panel are labeled File, Pattern, and Run.
The File button menu contains I/O options and "Exit". Within this menu, the following choices are available:
Selecting the load/save options will bring up a window asking for a directory and a filename. After this information is entered, the user can either click the "Apply" button to apply the input or "Cancel" button to discard the changes. Values entered for directory and filename will remain with the individual windows (i.e. a filename given to the Load Image window will appear the next time this window is displayed and won't appear for the other I/O windows).
The "Save Pattern..." choice is grayed out until there is a pattern in memory to save.
Files to be loaded must be in Sherlock internal format. Files are saved in this internal format.
The Pattern button menu contains choices for dealing with patterns. The "Select" choice will crop the pattern from the image. The mouse can be used to create a crop box (see Mouse Operations paragraph below). The "Display" choice will display a pattern that's in memory. Both choices are grayed out until needed (for "Select" that's creating a crop box, for "Display", that's having a pattern in memory to display).
FIGURE 8. Sherlock pattern menu
The Run button contains the algorithms to run. The four choices are: "Space Domain Correlation", "Frequency Domain Correlation", "Linear Pixel Shuffling", and "Random Ordering". This button is grayed out until there is a pattern in memory so that the algorithms can run.
FIGURE 9. Sherlock run menu
A gauge is displayed when an algorithm is being executed. This gauge displays how much of the algorithm run time has been spent and how much more there is to go.
FIGURE 10. Sherlock status gauge
Mouse Operations are as follows.The crop box used to select a pattern from the image is drawn by holding down the left button. The box can be stretched by moving the mouse with the left button held down. As soon as the left button is released, the crop box can no longer be adjusted. If the left button isn't being held down, the current mouse position is displayed in the right footer of the image window. This allows the user to see how good the algorithm worked to find the center location of the pattern.
The colormap is set to a grayscale colormap (and so the images are limited to 8 bit/pixel grayscale). Closest colors are used if a certain grayscale is unavailable (meaning that a white background can look slightly grayish). The data used in the calculations or saved to disk are the actual values, not the colormapped values.
A file of commands can be given to be interpreted. If a "-" (dash) is given as the filename for the "-b" option, commands are read from stdin.
The following commands are available:
(EQ 2)
where f is the pixel in subimage D and h is the image.
Sherlock then looks for a minimum to find the greatest correlation (i.e. the least difference between matrices). This speeds up the processing by not having to:
Also, by not having to subtract the average, Sherlock can do the subtraction with integers, not floating point numbers.
The steps for this algorithm are as follows:
In order for the Frequency Domain Correlation to work, Sherlock needs a black (pixel value 0) background with a non-black object. This is so zero padding of black can be applied to the pattern and image to boost the size to that of a power of 2 (so that the Fast Fourier Transform function can work as fast as possible). Therefore, the first pixel (location [0,0]) is checked to see if it's equal to 0. If it is, Sherlock assumes the background is black and the object is non-black. If it isn't, Sherlock inverts the image (or pattern). This assumes that the pattern won't be covering position (0,0). If it is, or some reason, the auto detection isn't working properly, the inversion behavior can be controlled by switches (-ii and -ip) and in the case of batch mode, by commands (invert type {yes|no|auto}).
The steps for this algorithm are as follows:
The pixel ordering is done so as to guarantee that every pixel location is visited only once.
The parameters were obtained from a table of suitable parameters.
The algorithm steps are the same as for SPACE DOMAIN (see above) except for the method of selecting the next pixel within the image (step 3). Instead, the change in position is calculated using the equations listed above.
FIGURE 11. block diagram of Sherlock and it's timer process
For the correlation data, the difference values (see Section 4.2 on page 14 which describes this) are saved during an algorithm's execution. After the algorithm is done, the following equation is used for Space Domain, LPS, and Random Ordering data to convert differences into normalized correlation values (from 0% to 100% correlation).
(EQ 3)
NCi is the normalized output data correlation value. Di is the difference value. P is the number of values. For Frequency Domain results, the data is normalized to compare to the other algorithm's results.
(EQ 4)
Since Frequency Domain calculates correlations (not differences), Ci is the correlation value.
For the first two experiments, an algorithm was claimed to have found a partial match when the distance became smaller than the initial distance value. This is reasonable since there was no noise in the image and the higher correlation values could only have come from matching the pattern. The LPS parameters used for these experiments were 509 and 557 for the maximum values and 237 and 380 for the increments for X and Y, respectively.
Because the image in Experiment 3 had noise (and therefore no sharp indication of partial success in the correlation), it wasn't enough to say that the algorithm had found the pattern when the distance became shorter. Instead, the Space Domain results were used to find the maximum distance from first contact with the pattern to the center. This was known because Space Domain first makes contact with a pattern at its boundary and then moves toward the center (which results in a delta function). This maximum distance was used as a threshold. Any algorithm that had a distance equal to or smaller than this threshold value was considered to be matching the pattern and not something else. For this experiment, 619 and 809 were the maximum values and 288 and 552 were the increments for X and Y, respectively.
For all three experiments, the center of the pattern was considered matched when the distance was equal to 0.
TABLE 1. first partial match found (in seconds)
-------------------------------
Case Space Freq Random LPS
-------------------------------
3x3 12 100 86 2
5x5 28 98 84 2
11x11 128 100 88 2
41x41 1,584 98 100 2
81x81 5,424 100 74 2
-------------------------------
TABLE 2. found pattern center (in seconds)
---------------------------------
Case Space Freq Random LPS
---------------------------------
3x3 12 100 96 8
5x5 28 100 116 14
11x11 130 100 194 62
41x41 1,768 100 1,920 812
81x81 6,866 100 5,376 3,136
---------------------------------
TABLE 3. first partial match found (in seconds)
-----------------------------------
Case Space Freq Random LPS
-----------------------------------
(102,17) 4 96 84 2
(148,157) 48 98 76 2
(182,59) 16 98 90 2
(196,36) 8 98 84 2
(202,248) 76 96 86 2
(226,327) 102 96 86 2
(290,201) 60 98 82 2
(293,138) 42 98 82 2
(354,168) 50 98 92 2
(368,291) 90 98 88 2
(374,13) 2 96 76 2
(387,5) 2 98 78 2
(408,67) 18 140 72 2
(432,338) 104 96 88 2
(444,251) 76 96 88 2
(447,36) 8 98 88 2
(466,392) 124 98 78 2
(489,174) 52 96 74 2
(63,48) 12 98 92 2
(91,321) 100 98 106 2
Averages 49.7 99.4 84.5 2
-----------------------------------
TABLE 4. found pattern center (in seconds)
------------------------------------
Case Space Freq Random LPS
------------------------------------
(102,17) 6 96 146 44
(148,157) 50 98 126 22
(182,59) 20 98 148 158
(196,36) 12 98 210 112
(202,248) 78 96 200 86
(226,327) 106 98 88 168
(290,201) 64 98 196 62
(293,138) 44 98 140 44
(354,168) 54 98 216 92
(368,291) 92 98 178 98
(374,13) 4 96 104 156
(387,5) 2 98 234 38
(408,67) 22 140 164 28
(432,338) 108 98 120 68
(444,251) 80 98 106 100
(447,36) 12 98 160 8
(466,392) 128 98 210 106
(489,174) 56 96 192 154
(63,48) 16 98 176 62
(91,321) 104 98 124 104
Averages 52.9 99.7 161.9 85.5
------------------------------------
TABLE 5. first partial match found (in seconds)
-------------------------------
Case Space Freq Random LPS
-------------------------------
text 10,186 550 844 98
-------------------------------
TABLE 6. found pattern center (in seconds)
---------------------------------
Case Space Freq Random LPS
---------------------------------
text 14,506 550 7,676 7,162
---------------------------------
TABLE 7. timing for Experiment 1 cases
------------------------------------------------------------------
Case # pixels Seconds/ Pixels/ # of pixels Seconds
Pixel Second til 1st
partial
match
------------------------------------------------------------------
3x3 200,400 5.9880E-05 16,700.0000 570 3.4132E-02
5x5 200,400 1.3972E-04 7,157.1429 570 7.9641E-02
11x11 200,400 6.4870E-04 1,541.5385 570 3.6976E-01
41x41 200,400 8.8224E-03 113.3484 5 4.4112E-02
81x81 200,400 3.4261E-02 29.1873 5 1.7131E-01
------------------------------------------------------------------
For the table above, column 1 is the case (in terms of pattern size). Column 2 is the number of pixels to go through to get to the center of the pattern. Column 3 is the seconds/pixel rate based upon the number of pixels and the time it took to process them. For example, for the first case (3x3), we know from Table 2 on page 18 that it took 12 seconds for Space Domain to find the center. Since the center is at (400,400), we know column 2 to be 200,400 pixels. Just divide 12 by 200,400 to get the seconds/pixel rate. Column 4 is the inverse of column 3 to show the pixels/second rate. Column 5 is the number of pixels that had to be processed by LPS until a partial match was made. This is determined by looking at the pixel ordering that LPS went through. Since the same parameters were used for LPS in Experiments 1 and 2, this ordering will be constant. Column 6 is the number of seconds it took to get through the number of pixels listed in column 5.Since each case has a different sized pattern, the time it takes to calculate the correlation at each pixel location in the image is different. The bigger the pattern, the more calculations are needed, the longer the time (as shown in columns 3 and 4). Column 6 is based on the individual times for each cases.
As can be seen in column 6, LPS finds a partial match in well under 2 seconds.
FIGURE 12. Pattern Size vs. Number of seconds to find a partial match in Experiment 1
Figure 12 on page 22 shows the pattern size vs. the number of seconds it took an algorithm to find a partial match. This graph shows LPS, Frequency Domain, and Random Ordering to be pixel size invariant (with LPS being the quickest of the three) compared to Space Domain which is dependent on pattern size.
TABLE 8. timing for Experiment 2 cases
----------------------------------------------------------------------
Case # pixels Seconds/ Pixels/ # of pixels Seconds
Pixel Second til 1st
partial
match
----------------------------------------------------------------------
(102,17) 8,602 6.9751E-04 1,433.6667 98 6.3374E-02
(148,157) 78,648 6.3574E-04 1,572.9600 583 3.7701E-01
(182,59) 29,682 6.7381E-04 1,484.1000 160 1.0347E-01
(196,36) 18,196 6.5949E-04 1,516.3333 4 2.5867E-03
(202,248) 124,202 6.2801E-04 1,592.3333 555 3.5891E-01
(226,327) 163,726 6.4742E-04 1,544.5849 412 2.6643E-01
(290,201) 100,790 6.3498E-04 1,574.8438 191 1.2352E-01
(293,138) 69,293 6.3498E-04 1,574.8409 525 3.3951E-01
(354,168) 84,354 6.4016E-04 1,562.1111 151 9.7648E-02
(368,291) 145,868 6.3071E-04 1,585.5217 279 1.8042E-01
(374,13) 6,874 5.8190E-04 1,718.5000 60 3.8801E-02
(387,5) 2,887 6.9276E-04 1,443.5000 416 2.6902E-01
(408,67) 33,908 6.4881E-04 1,541.2727 442 2.8583E-01
(432,338) 169,432 6.3742E-04 1,568.8148 338 2.1858E-01
(444,251) 125,944 6.3520E-04 1,574.3000 159 1.0282E-01
(447,36) 18,447 6.5051E-04 1,537.2500 43 2.7807E-02
(466,392) 196,466 6.5151E-04 1,534.8906 362 2.3410E-01
(489,174) 87,489 6.4008E-04 1,562.3036 604 3.9059E-01
(63,48) 24,063 6.6492E-04 1,503.9375 63 4.0741E-02
(91,321) 160,591 6.4761E-04 1,544.1442 638 4.1258E-01
Averages 82,473.10 6.4668E-04 1,548.5105 304.15 1.9669E-01
----------------------------------------------------------------------
The descriptions for the columns are the same as for the table in the last section. Column 1 lists the cases in terms of pattern centers. Unlike Experiment 1, the pattern is the same size for all cases. This should lead us to believe the timings for columns 3 and 4 should be the same. They do differ by a small amount. The mean for seconds/pixel is 6.4668E-04. This is roughly 26 times greater than the standard deviation (2.4581E-05). Column 6's results are based on this mean value.Again, it can be seen that LPS finds a partial match under 2 seconds.
The results for Frequency Domain in the 408x67 case obviously don't seem to belong. This anomaly is explained by background processes running at the same time. Repeat trials of this case show the results to be similar to other case results.
TABLE 9. results for 5 retrials of case 408x67 for partial match (in seconds)
-----------------------------------
Case Space Freq Random LPS
-----------------------------------
retrial 1 20 99 42 2
retrial 2 18 99 39 2
retrial 3 18 98 114 2
retrial 4 18 98 82 2
retrial 5 20 99 80 2
means 18.8 98.6 71.4 2
-----------------------------------
TABLE 10. results for 5 retrials of case 408x67 for pattern center (in
seconds)
------------------------------------
Case Space Freq Random LPS
------------------------------------
retrial 1 24 99 120 28
retrial 2 22 99 158 28
retrial 3 22 98 268 26
retrial 4 22 98 176 26
retrial 5 22 99 100 28
means 22.4 98.6 164.4 27.2
------------------------------------
The same approximate values resulted for Space Domain, LPS, and Random Order as in the original test case. Rerunning this particular case shows that the 140 seconds for Frequency Domain from the original experiment is not correct. The mean values for Frequency Domain are close to other case results, as expected.FIGURE 13. Position vs. Number of seconds to find a partial match in Experiment 2
Figure 13 on page 25 shows the position vs. the number of seconds it took an algorithm to find a partial match. Position is in terms of sequential order (i.e. for a 500x500 pixel image, pixel (1,1) is the 501th pixel). This graph shows LPS, Frequency Domain, and Random Ordering to be position invariant (with LPS being the quickest of the three). Space Domain is shown to be dependent on position.
TABLE 11. timing for Experiment 3 case
-------------------------------------------------------------
Case # pixels Seconds/ Pixels/ # of pixels Seconds
Pixel Second til 1st
partial
match
-------------------------------------------------------------
text 314,061 4.6188E-02 21.6504 2,089 9.6488E+01
-------------------------------------------------------------
The descriptions for the columns are the same as for the table in the first section. Comparing the number of seconds in column 6 (~96.5 seconds) to the number of seconds LPS took to find a partial match in Table 5 on page 20 (98 seconds), we see that the values for LPS in Table 5 are indeed correct.
TABLE 12. speed ratio (in seconds) for Experiment 1 for finding a partial
match
--------------------------------------
Case Space/LPS Freq/LPS Random/LPS
--------------------------------------
3x3 6 50 43
5x5 14 49 42
11x11 64 50 44
41x41 792 49 50
81x81 2712 50 37
--------------------------------------
Since the pattern size is the same in all cases for Experiment 2, the timing difference can be averaged. On average, LPS found a partial match 47.7, 97.4, and 82.5 seconds faster than Space Domain, Frequency Domain, and Random Ordering, respectively for finding a partial match.
TABLE 13. speed ratio (in seconds) for Experiment 2 for finding a partial
match
------------------------------------------
Case Space/LPS Freq/LPS Random/LPS
------------------------------------------
(102,17) 2 48 42
(148,157) 24 49 38
(182,59) 8 49 45
(196,36) 4 49 42
(202,248) 38 48 43
(226,327) 51 48 43
(290,201) 30 49 41
(293,138) 21 49 41
(354,168) 25 49 46
(368,291) 45 49 44
(374,13) 1 48 38
(387,5) 1 49 39
(408,67) 9 70 36
(432,338) 52 48 44
(444,251) 38 48 44
(447,36) 4 49 44
(466,392) 62 49 39
(489,174) 26 48 37
(63,48) 6 49 46
(91,321) 50 49 53
Averages 24.85 49.7 42.25
------------------------------------------
Below are the difference values for Experiment 3 for finding a partial match.
TABLE 14. speed ratio (in seconds) for Experiment 3 for finding a partial match ------------------------------------ Case Space/LPS Freq/LPS Random/LP ------------------------------------ text 104 6 9 ------------------------------------
This project did not investigate the effects of image/pattern noise. However, the single real test case examined suggests that LPS may yield similar processing speed improvements when noise is present.
Despite the fact that LPS took longer to find the exact center (in some cases), LPS is useful as a subpattern searching algorithm. Intelligent processing can be added to allow LPS to find the center much faster than is shown here. LPS has consistently demonstrated that it has the capability to find a pattern much quicker than the other algorithms in this project.
The work done here in no way shows the full potential of LPS. In a real application, once the pattern's neighborhood is found, there would be no need to continue looking at every pixel as was done here. This experiment merely lays down the foundation to show that LPS is an algorithm that can be made use of for subpattern searching.
One problem seen with LPS is when there is an unknown number of patterns. LPS's strength is the ability to find a match quickly. When the number of patterns is not known in advance, the question arises as to when LPS should stop searching.
One way to improve performance is to zero in when that first partial match is found. Instead of continuing, concentrate on the specific area the match was found by doing the LPS algorithm on this sub-sample.
Another way to speedup performance is to improve the correlation calculation. Any way to speed up the calculation would speedup the whole process.
Noise was not really an issue in this project. The first 2 experiments were noise-free. One direction to go with LPS research is to look into how it handles noise. Given the first 2 experiments with noise, the same results would be expected. It's with intelligent processing that noise becomes more troublesome. What happens when you get some correlation? Should LPS investigate the sub-sample? Or is the correlation only noise and LPS would be wasting its time? Also, if LPS is trying to zero in on the center, how long should it process before it realizes that the pattern isn't in the sub-sample? One way to get around these problems would be to set a threshold. Any correlation above this threshold would be considered pattern, anything below would be noise.
In the case of an unknown number of patterns, an intelligent processing algorithm to look into is to setup the LPS parameters based on the size of the pattern so that you are likely to hit a pattern (if one exists) on every jump. One pass through the image would tell you the correlation hot spots to zero in on.
There are several different methods to find parameters for LPS. Another area to look into is to discover which method produces the best parameters.