Linear Pixel Shuffling

Linear Pixel Shuffling (LPS) is a method to get a semi-random ordering of pixels. Unlike other techniques, LPS creates a pixel ordering that is spread evenly across the image. It wraps around the image by use of modular arithmetic. A simple arithmetic progression is needed to determine the next pixel location.

Objective

The objective of this project is to compare Linear Pixel Shuffling (LPS) as a Pattern Recognition tool, against more traditional algorithms that are based on Space and Frequency Domain Correlation. The study will demonstrate the speed and efficiency of LPS as a potentially enhanced method for Pattern Recognition.

Outline

Introduction
Procedure
Results
Conclusions

Experimental Rational

Why compare LPS to Space Domain?

- Traditional textbook algorithm

- Same correlation equation

- Used for large ratio problems

Why compare LPS to Frequency Domain?

- Used for small ratio problems

Why compare LPS to Random Ordering?

- Compare "pseudo-random" ordering of LPS against "true-random" ordering

Space Domain

Frequency Domain

Random Ordering

Linear Pixel Shuffling

Outline

Introduction
Procedure
Results
Conclusions

Algorithm Implementation

Space Domain

Space Domain isn't implemented in the traditional way. Instead, this algorithm sums the absolute value of the difference between corresponding pixels.

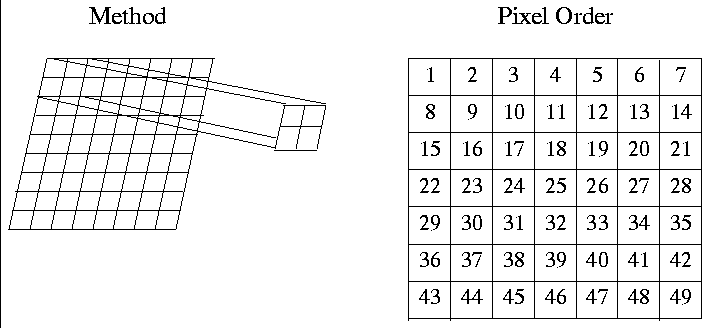
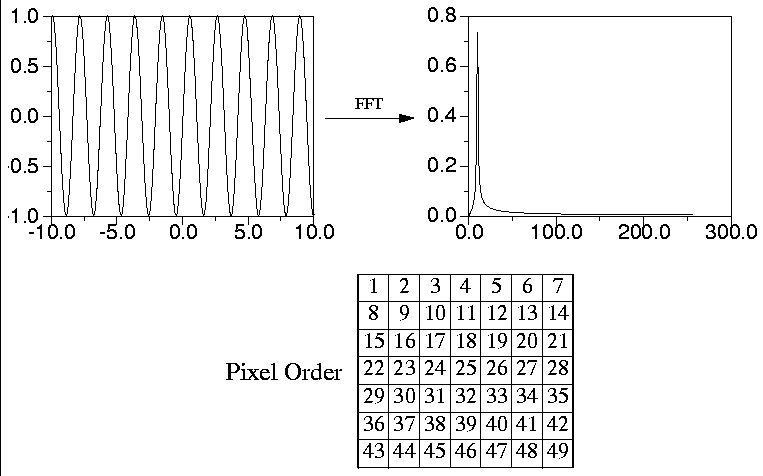
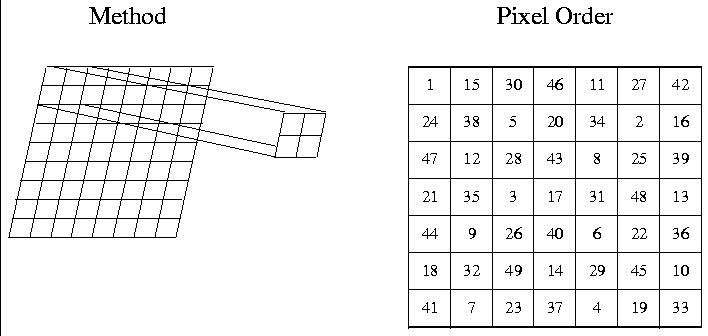
Advantages to this method are:

Subtraction of average not necessary
Perform calculations with integer rather than floating point data

The algorithm steps are:

At [row = 0, col = 0], find the difference
Check difference value for minimum
Move to the next pixel location until every pixel in the image is sampled

Algorithm Implementation (cont.)

Frequency Domain

In order to save time, no beercanning or checkerboarding is done. The FFT routine assumes the 0 point to be in the middle, and the software uses this point as the first element in the array. Consequently, the inverse FFT will show the highest correlation in the upper left corner of the pattern.
The software needs a black (pixel value 0) background with a non-black pattern. Autorecognition is used to determine if pattern and/or image must be inverted.

Algorithm Implementation (cont.)

The steps for this algorithm are as follows:

Determine 2N size equal to or greater than the largest dimension of the pattern and image
Zero pad pattern and image to the size determined in (1)
Calculate Fourier Transform of image and pattern
Multiply the FFT of the image and pattern on a pixel-by-pixel basis
Take the inverse Fourier Transform of multiplication
Search for a maximum in the inverted transform results

Algorithm Implementation (cont.)

Random Ordering

Same steps as Space Domain except that the selection of the next pixel is totally random.

Algorithm Implementation (cont.)

Linear Pixel Shuffling

Instead of a sequential pixel ordering, change in position is calculated by:

% indicates modulus operation
X increment, Y increment, xmax, and ymax are parameters affecting the pixel ordering.
The parameters used in this project came from a list of prime numbers.
Same steps as Space Domain with the exception being the selection of the next pixel.

Software Implementation

Sherlock

Sherlock is an Open Look\xaa application that can read in an image and pattern and run the 4 algorithms.

Written in C on a Sun 4/40
Uses the XView toolkit
Fast Fourier Transform routine originally written in Fortran by Norman Brenner in 1968. Code translated to C by Keith Knox of Xerox Webster Research Center, September 1990
Timing macros written by George V. Neville-Neil, Universiteit Twente
Implements Space Domain, Frequency Domain, Random Ordering, and LPS

Software Implementation (cont.)

After an algorithm has run, information about it is presented. In Batch Mode, it is written to the screen. In UI Mode, a window pops up with the information. Both cases provide the following:

Test - Name of algorithm

Ratio - ratio between image and pattern (image:pattern)

Time - algorithm runtime (h:m:s)

Pos - Location of a match

Image - filename of the image

Pattern - filename of the pattern (or from image if cropped)

Software Implementation (cont.)

Tools used:

CodeCenter (programming environment by CenterLine Software, Inc.)
FrameMaker (publishing tool by Frame Technology Corporation)
Lotus (spreadsheet by Lotus Development Corporation)
Ace/gr (free 2D graphing program for exploratory data analysis written by Paul Turner; xvgr is the xview version)
Xerox in-house software

Common Experimental Elements

4 algorithms were used
Euclidean distance values were obtained every 2 seconds.
Euclidean distances were compared.
Correlation values were plotted.

Experiments

Experiment 1

Objective

Ascertain if LPS had any speed advantage.

Experimental Conditions

Keep the center of the pattern constant while the size is changed.
Five pattern sizes were: 3x3, 5x5, 11x11, 41x41, and 81x81. The image is 500x500.

Experiments (cont.)

Experiment 2

Objective

Establish shift invariance of LPS.

Experimental Conditions

Keep the pattern size the same and move the pattern around the image.
Pattern size is 11x11. The image size is 500x500.
Experiment 2 had 20 cases.

Experiments (cont.)

Experiment 3

Objective

Determine the influence of image/pattern noise on LPS(1).

Experimental Conditions

Image consists of a scanned-in page of text. The pattern is a circle created by a rubber stamp.
Image size is 612x792. The pattern size is 94x95.

Outline

Introduction
Procedure
Results
Conclusions

Outline

Introduction
Procedure
Results
Conclusions

Conclusions

LPS was the most efficient Pattern Recognition algorithm. Compared to other methods, LPS was:
- 5 - 2700x faster for pattern size dependence
- 24 - 41x faster for pattern position dependence
- 5 - 103x faster for a real test case
Results show that LPS is independent of position and pattern size

Limitations

This project did not investigate the effects of image/pattern noise. However, results from the single real test case suggest that LPS may calculate erroneous correlations in the presence of noise.
LPS algorithm used is insufficient to deal with an unknown number of patterns
Due to the ą1 second time resolution, the inherent efficiency of LPS may be greater than values determined in this project

Future Research

Add intelligent processing to:
- handle an unknown number of patterns
- find a pattern center quicker by concentrating on areas with high correlations
Expand the study to include the effects of noise
Expand the study of other techniques for obtaining LPS parameters to evaluate their efficiency

Numerical Results

Experiment 1

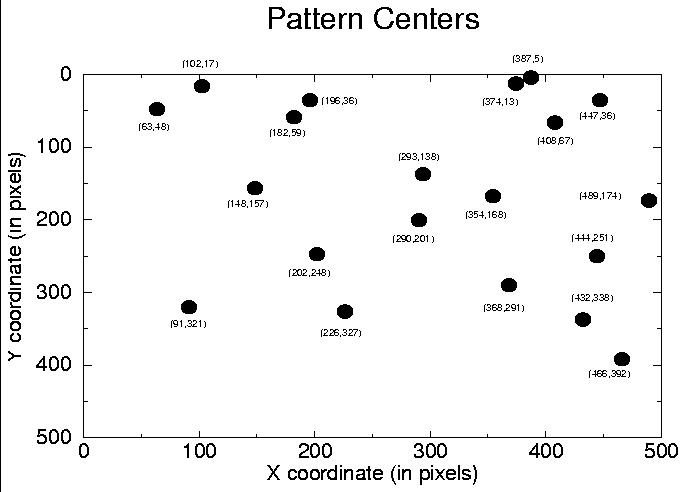
TABLE 1. first partial match found 
-------------------------------
Case   Space  Freq  Random  LPS  
-------------------------------
3x3    12     100   86      2    
5x5    28     98    84      2    
11x11  128    100   88      2    
41x41  1,584  98    100     2    
81x81  5,424  100   74      2    
                                 
-------------------------------

TABLE 2. found pattern center 
---------------------------------
Case   Space  Freq  Random  LPS    
---------------------------------
3x3    12     100   96      8      
5x5    28     100   116     14     
11x11  130    100   194     62     
41x41  1,768  100   1,920   812    
81x81  6,866  100   5,376   3,136  
                                   
---------------------------------

Numerical Results (cont.)

Experiment 2

TABLE 3. first partial match found (in seconds) 
-----------------------------------
Case       Space  Freq  Random  LPS  
-----------------------------------
(102,17)   4      96    84      2    
(148,157)  48     98    76      2    
(182,59)   16     98    90      2    
(196,36)   8      98    84      2    
(202,248)  76     96    86      2    
(226,327)  102    96    86      2    
(290,201)  60     98    82      2    
(293,138)  42     98    82      2    
(354,168)  50     98    92      2    
(368,291)  90     98    88      2    
(374,13)   2      96    76      2    
(387,5)    2      98    78      2    
(408,67)   18     140   72      2    
(432,338)  104    96    88      2    
(444,251)  76     96    88      2    
(447,36)   8      98    88      2    
(466,392)  124    98    78      2    
(489,174)  52     96    74      2    
(63,48)    12     98    92      2    
(91,321)   100    98    106     2    
                                     
-----------------------------------

Numerical Results (cont.)

TABLE 4. found pattern center (in seconds) 
-----------------------------------
Case       Space  Freq  LPS  Random  
-----------------------------------
(102,17)   6      96    44   146     
(148,157)  50     98    22   126     
(182,59)   20     98    158  148     
(196,36)   12     98    112  210     
(202,248)  78     96    86   200     
(226,327)  106    98    168  88      
(290,201)  64     98    62   196     
(293,138)  44     98    44   140     
(354,168)  54     98    92   216     
(368,291)  92     98    98   178     
(374,13)   4      96    156  104     
(387,5)    2      98    38   234     
(408,67)   22     140   28   164     
(432,338)  108    98    68   120     
(444,251)  80     98    100  106     
(447,36)   12     98    8    160     
(466,392)  128    98    106  210     
(489,174)  56     96    154  192     
(63,48)    16     98    62   176     
(91,321)   104    98    104  124     
                                     
-----------------------------------

Numerical Results (cont.)

Experiment 3

TABLE 5. first partial match found (in seconds) 
-------------------------------
Case  Space   Freq  Random  LPS  
-------------------------------
text  10,186  550   844     98   
                                 
-------------------------------

TABLE 6. found pattern center (in seconds) 
---------------------------------
Case  Space   Freq  Random  LPS    
---------------------------------
text  14,506  550   7,676   7,162  
---------------------------------

Numerical Analysis of Results

Experiment 1

TABLE 7. timing for Experiment 1 cases 
------------------------------------------------------------------
Case   # pixels  Seconds/    Pixels/      # of pixels   Seconds     
                 Pixel       Second       til 1st                   
                                          partial                   
                                          match                     
------------------------------------------------------------------
3x3    200,400   5.9880E-05  16,700.0000  570           3.4132E-02  
5x5    200,400   1.3972E-04  7,157.1429   570           7.9641E-02  
11x11  200,400   6.4870E-04  1,541.5385   570           3.6976E-01  
41x41  200,400   8.8224E-03  113.3484     5             4.4112E-02  
81x81  200,400   3.4261E-02  29.1873      5             1.7131E-01  
                                                                    
------------------------------------------------------------------

Numerical Analysis of Results (cont.)

Experiment 2

TABLE 8. timing for Experiment 2 cases 
--------------------------------------------------------------------
Case       # pixels  Seconds/    Pixels/    # of pixels   Seconds     
                     Pixel       Second     til 1st                   
                                            partial                   
                                            match                     
--------------------------------------------------------------------
(102,17)   8,602     6.9751E-04  1433.6667  98            6.3374E-02  
(148,157)  78,648    6.3574E-04  1572.9600  583           3.7701E-01  
(182,59)   29,682    6.7381E-04  1484.1000  160           1.0347E-01  
(196,36)   18,196    6.5949E-04  1516.3333  4             2.5867E-03  
(202,248)  124,202   6.2801E-04  1592.3333  555           3.5891E-01  
(226,327)  163,726   6.4742E-04  1544.5849  412           2.6643E-01  
(290,201)  100,790   6.3498E-04  1574.8438  191           1.2352E-01  
(293,138)  69,293    6.3498E-04  1574.8409  525           3.3951E-01  
(354,168)  84,354    6.4016E-04  1562.1111  151           9.7648E-02  
(368,291)  145,868   6.3071E-04  1585.5217  279           1.8042E-01  
(374,13)   6,874     5.8190E-04  1718.5000  60            3.8801E-02  
(387,5)    2,887     6.9276E-04  1443.5000  416           2.6902E-01  
(408,67)   33,908    6.4881E-04  1541.2727  442           2.8583E-01  
(432,338)  169,432   6.3742E-04  1568.8148  338           2.1858E-01  
(444,251)  125,944   6.3520E-04  1574.3000  159           1.0282E-01  
(447,36)   18,447    6.5051E-04  1537.2500  43            2.7807E-02  
(466,392)  196,466   6.5151E-04  1534.8906  362           2.3410E-01  
(489,174)  87,489    6.4008E-04  1562.3036  604           3.9059E-01  
(63,48)    24,063    6.6492E-04  1503.9375  63            4.0741E-02  
(91,321)   160,591   6.4761E-04  1544.1442  638           4.1258E-01  
                                                                      
--------------------------------------------------------------------

Numerical Analysis of Results (cont.)

The results for Frequency Domain in the 408x67 case obviously don't seem to belong. This anomaly is explained by background processes running at the same time. Repeat trials of this case show the results to be similar to other case results.

TABLE 9. results for 5 retrials of case 408x67 for partial match 
-----------------------------------
Case       Space  Freq  Random  LPS  
-----------------------------------
retrial 1  20     99    42      2    
retrial 2  18     99    39      2    
retrial 3  18     98    114     2    
retrial 4  18     98    82      2    
retrial 5  20     99    80      2    
means      18.8   98.6  71.4    2    
                                     
-----------------------------------

TABLE 10. results for 5 retrials of case 408x67 for pattern center 
------------------------------------
Case       Space  Freq  Random  LPS   
------------------------------------
retrial 1  24     99    120     28    
retrial 2  22     99    158     28    
retrial 3  22     98    268     26    
retrial 4  22     98    176     26    
retrial 5  22     99    100     28    
means      22.4   98.6  164.4   27.2  
                                      
------------------------------------

The same approximate values resulted for Space Domain, LPS, and Random Order as in the original test case. Rerunning this particular case shows that the 140 seconds from the original experiment is not correct. The mean values for Frequency Domain are close to other case results, as expected.

Numerical Analysis of Results (cont.)

Experiment 3

TABLE 11. timing for Experiment 3 case 
-------------------------------------------------------------
Case  # pixels  Seconds/    Pixels/  # of pixels   Seconds     
                Pixel       Second   til 1st                   
                                     partial                   
                                     match                     
-------------------------------------------------------------
text  314,061   4.6188E-02  21.6504  2089          9.6488E+01  
                                                               
-------------------------------------------------------------

Footnotes

(1): This experiment was performed to demonstrate the use of LPS with typical images. It is not intended to demonstrate the effect of image noise. A detailed study of LPS and noise is beyond the scope of this project

Linear Pixel Shuffling

and

Pattern Recognition

Table of Contents

Footnotes